“Racorn-k”版本间的差异
(→Experiments on several datasets) |
(→Reference) |
||
| 第107行: | 第107行: | ||
=Reference= | =Reference= | ||
| − | [1] | + | [1] Bin Li, Steven CH Hoi, and Vivekanand Gopalkrishnan, “Corn: Correlation-driven nonparametric learning approach for portfolio selection,”, ACM Transactions on Intelligent Systems and Technology (TIST), vol. 2, no. 3,pp. 21, 2011. |
| − | [2] | + | [2] Thomas M Cover and David H Gluss, “Empirical bayes stock market portfolios,” Advances in applied mathematics, vol. 7, no. 2, pp. 170–181, 1986. |
| − | + | ||
| − | [3] | + | [3] B Li, D Sahoo, and SCH Hoi, “Olps: A toolbox for online portfolio selection,” Journal of Machine Learning Research (JMLR), 2015. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
2017年10月31日 (二) 06:47的版本
目录
Project name
RACORN-K: Risk-aversion Pattern Matching-based Portfolio Selection
Project members
Yang Wang, Dong Wang, Yaodong Wang, You Zhang
Introduction
Portfolio selection is the central task for assets management, but it turns out to be very challenging. Methods based on pattern matching, particularly the CORN-K algorithm, have achieved promising performance on several stock markets. A key shortage of the existing pattern matching methods, however, is that the risk is largely ignored when optimizing portfolios, which may lead to unreliable profits, particularly in volatile markets. To make up this shortcoming, We propose a risk-aversion CORN-K algorithm, RACORN-K, that penalizes risk when searching for optimal portfolios. Experiment results demonstrate that the new algorithm can deliver notable and reliable improvements in terms of return, Sharp ratio and maximum drawdown, especially on volatile markets.
Corn-k
Corn-k algorithm is proposed by Li et al.[1]. At the t-th trading period, the CORN-K algorithm first selects all the historical periods whose market status is similar to that of the present market, where the similarity is measured by the Pearson correlation coefficient. This patten matching process produces a set of similar periods, which we denote by C. Then do a optimization following the idea of BCRP[2] on C. Finally, the outputs of the top-k experts that have achieved the highest accumulated return are weighted to derive the ensemble-based portfolio.
Racorn-k
The portfolio optimization is crucial for the success of CORN-K. A potential problem of the existing form, however, is that the optimization is purely profit-driven. A natural idea to consider the risk is to penalize risky portfolios when searching for the optimal portfolio. We use the standard deviation of log return on C to represent the risk and subtract this term as penalty.
Racorn(c)-k
The combination method used in CORN-K does not consider the time-variant property of the risk. In fact, the risk of the portfolio derived from each expert tends to change quickly in an volatile market and therefore the weights of individual experts should be adjusted timely. To achieve the quick adjustment, we use the instant return st(w,ρ,λ) to weight the experts with different λ, rather than the accumulated return. Since st is not available when estimating the optimal portfolio , we approximate it by the geometric average of the returns achieved in C.
Experiments on several datasets
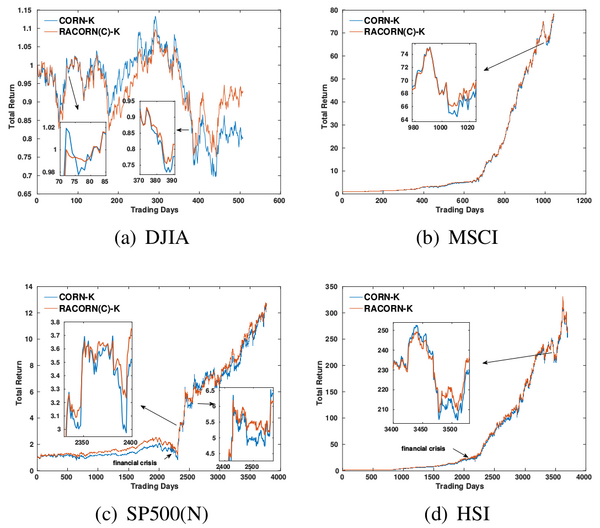
We evaluate our proposed algorithm on several dataset: DJIA, MSCI, SP500(N), HSI, SP500(O). DJIA, MSCI and SP500(O) are open dataset[3] that are used in previous work. you can find it here. To observe the performance on more recent market, we collected another two dataset: SP500(N) and HSI (download). Form the following table, we can see that our algorithm can improve Sharpe ratio and reduce maximum drawdown consistently. In most case, it can also achieve better accumulated return.
------------------------------------------------------------------------------------------------------------------
| Dataset DJIA MSCI SP500(N) HSI SP500(O)
------------------------------------------------------------------------------------------------------------------
| Criteria RET SR MDD | RET SR MDD | RET SR MDD | RET SR MDD | RET SR MDD
Main |RACORN(C)-K 0.93 0.01 0.32 | 78.38 3.73 0.21 | 12.55 0.77 0.53 | 202.04 1.60 0.28 | 7.13 1.28 0.34
Results | RACORN-K 0.83 -0.19 0.37 | 79.52 3.67 0.21 | 13.03 0.72 0.57 | 264.02 1.60 0.29 | 9.27 1.33 0.32
| CORN-K 0.80 -0.24 0.38 | 77.54 3.63 0.21 | 12.50 0.70 0.60 | 254.27 1.56 0.30 | 8.72 1.26 0.35
------------------------------------------------------------------------------------------------------------------
Naive | UBAH 0.76 -0.43 0.39 | 0.90 0.02 0.65 | 1.52 0.24 0.50 | 3.54 0.53 0.58 | 1.33 0.36 0.46
Methods | UCRP 0.81 -0.28 0.38 | 0.92 0.05 0.64 | 1.78 0.28 0.68 | 4.25 0.58 0.55 | 1.64 0.55 0.31
------------------------------------------------------------------------------------------------------------------
Follow the | UP 0.81 -0.29 0.38 | 0.92 0.04 0.64 | 1.79 0.29 0.68 | 4.26 0.59 0.55 | 1.66 0.56 0.31
Winner | EG 0.81 -0.29 0.38 | 0.92 0.04 0.64 | 1.75 0.28 0.67 | 4.22 0.58 0.55 | 1.62 0.54 0.32
| ONS 1.53 0.80 0.32 | 0.85 0.02 0.68 | 0.78 0.27 0.96 | 4.42 0.52 0.68 | 3.32 1.11 0.25
------------------------------------------------------------------------------------------------------------------
| ANTICOR 1.62 0.85 0.34 | 2.75 0.96 0.51 | 1.16 0.24 0.93 | 9.10 0.74 0.56 | 5.58 1.08 0.38
| ANTICOR2 2.28 1.24 0.35 | 3.20 1.02 0.48 | 0.71 0.22 0.97 | 12.27 0.77 0.55 | 5.86 1.01 0.49
Follow the | PAMR2 0.70 -0.15 0.76 | 16.73 2.07 0.54 | 0.01 -0.28 1.00 | 1.19 0.20 0.86 | 4.97 0.90 0.51
Loser | CWMR Stdev 0.69 -0.17 0.76 | 17.14 2.07 0.54 | 0.02 -0.26 0.99 | 1.28 0.22 0.85 | 5.92 0.96 0.51
| OLMAR1 2.53 1.16 0.37 | 14.82 1.85 0.48 | 0.03 -0.11 1.00 | 4.19 0.46 0.77 | 15.89 1.28 0.41
| OLMAR2 1.16 0.40 0.58 | 22.34 2.08 0.42 | 0.03 -0.11 1.00 | 3.65 0.43 0.84 | 9.54 1.08 0.49
------------------------------------------------------------------------------------------------------------------
Pattern | BK 0.69 -0.68 0.43 | 2.62 1.06 0.51 | 1.97 0.31 0.59 | 13.90 0.88 0.45 | 2.21 0.64 0.49
Matching | BNN 0.88 -0.15 0.31 | 13.40 2.33 0.33 | 6.81 0.67 0.41 | 104.97 1.40 0.33 | 3.05 0.76 0.45
------------------------------------------------------------------------------------------------------------------
View the impact of risk-aversion
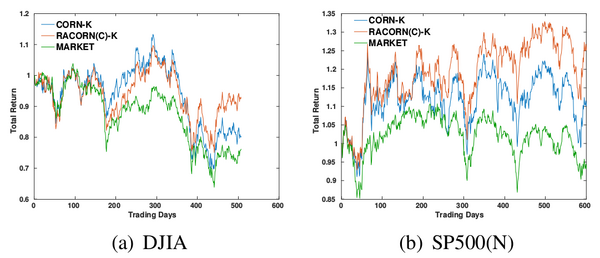
From RET curves we can see that RACORN(C)-K behaves more ‘smooth’ than CORN-K. Due to this smoothness, the risk of the strategy is reduced, and extremely poor trading can be largely avoided.
View the impact of risk-aversion on volatile markets
On volatile markets, our proposed algorithms are more effective.
Reference
[1] Bin Li, Steven CH Hoi, and Vivekanand Gopalkrishnan, “Corn: Correlation-driven nonparametric learning approach for portfolio selection,”, ACM Transactions on Intelligent Systems and Technology (TIST), vol. 2, no. 3,pp. 21, 2011.
[2] Thomas M Cover and David H Gluss, “Empirical bayes stock market portfolios,” Advances in applied mathematics, vol. 7, no. 2, pp. 170–181, 1986.
[3] B Li, D Sahoo, and SCH Hoi, “Olps: A toolbox for online portfolio selection,” Journal of Machine Learning Research (JMLR), 2015.